Ապրիլ ամսվա աշխատանքները
Երկրաչափություն-Դաս 34,35,36
Այս շաբաթվա ընթացքում կուղարկեմ քանի որ նոր ենք անում այս դասը։
Այս ամիս մեր ուսուցումը հեռավար էր, սկզբում դժվար էր ասել, թե ինչպես կանցնեն այս տարբերակով կատարված դասերը, բայց մի քանի օր անց, արդեն բավականին առաջընթաց կար՝ չհաշված որոշ տեխնիկական խնդիրները։ Եթե անցնենք իքնագնահատականին, ապա ես ինձ կնշանակեի 7, քանի որ շարունակում եմ աշխատել այնպես ինչպես միշտ աշխատել եմ և փորձում եմ ավելինն անել և տրված թեմաները հնարավորինս արդյունավետ յուրացնել։

1. Լուծիր համակարգը՝
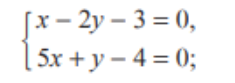
{x-2y=3
{5x+y=4
x=3+2y
5(3+2y)+y=4
15+10y+y=4
11y=(-11)
y=(-1)
x=3-2=1
(-1; 1)
2. Լուծիր խնդիրը՝

{x-y=4
{2x+2y=52
x=4+y
2(4+y)+2y=52
8+2y+2y=52
4y=44
y=11
x=4+11=15
(11; 15)
3. Պարզեցրու՝
ա)
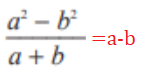
բ)
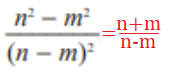
գ)
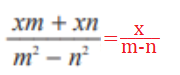
դ)
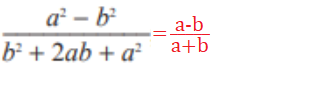
ե)
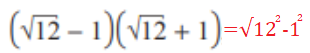
4. Լուծիր հավասարումները՝
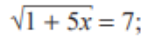
1+5x=49
5x=48
x=8
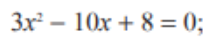
D=100-96
x1=10+2/6=2
x2=10-2/6=4/3
(4/3; 2)
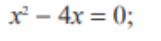
x(x-4)=0
x=0
x-4=0
x=4
(0; 4)
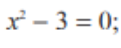
x²=3
x=√3
5. Լուծիր խնդիրը՝

{x+y=10
{x*y=21
x=10-y
(10-y)*y=21
10y-y²=21
10y-y²-21=0
-y²+10y-21=0
y²-10y+21=0
D=100-84=16
x1=10+4/2=7
x2=10-4/2=3
(3; 7)
Առ․ 632-635
632. ա) x²-6x+8=0
D=9-8=1
x1=3-√1/1=2
x2=3+√1/1=4
2; 4
բ) x²-2x-15=0
D=1+15=16
x1=1-√16/1=-3
x2=1+√16/1=5
-3; 5
գ) x²+6x+8=0
D=9-8=1
x1=-3-√1/1=-4
x2=-3+√1/1=-2
-4; -2
դ) x²+2x-15=0
D=1+15=16
x1=-1-√16/1=-5
x2=-1+√16/1=-3
-3; -5
ե) x²+20x+51=0
D=100-51=49
x1=-10-√49/1=-17
x2=-10+√49/1=-3
-17; -3
զ) x²-22x-23=0
D=121+23=144
x1=11-√144/1=-1
x2=11+√144/1=23
-1; 23
է) x²-20x+69=0
D=100-69=31
x1=10-√31/1
x2=10+√31/1
10-√31/1; 10+√31/1
ը) x²+22x+21=0
D=121-21=100
x1=-11-√100/1=-21
x2=-11+√100/1=-1
-21; -1
633. ա) x²-4x+4=0
D=4-4=0
x1=2-√0/1=2
x=2
բ) x²-8x+20=0
D=16-20=-4
∅
գ) x²-2.1/2x+1=0
D=4-4=0
x1=2-√0/1=2
x=2
Քառակուսի հավասարման լուծումը, երբ b-ն զույգ թիվ է՝
ax²+bx+c=0
a≠0
D=b²-4ac
x1=-b-√D/2a
x2=-b+√D/2a
D1=b/2²-ac
x1=-b/2-√D/a
x2=-b/2+√D/a
x²+6x+8=0
D=9-8=1
x1=-3-√1/1=-4
x2=-3+√1/1=-2
-4; -2
1.
tgA=1 => <A=45°, => <B=45°
2.
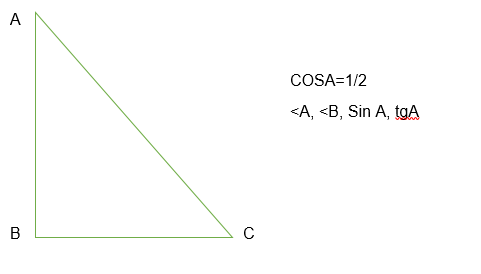
<A=60°
<B=30°
SinA=√3/2
tgA=√3
3.

a2=c2-b2=√25-√16=√9=3
SinB=3/5
COSB=CB/AB=4/5
tgA=4/3
Առ․ 602, 603, 604, 607
ա) 2x2=3
x2=1,5
x=±√1,5
բ) x2-9=0
x2=9
x=±3
գ) x2-25=0
x2=25
x=±5
դ) 16-x2=0
-x2=-16
x2=16
x=±4
ե) 49-x2=0
-x2=-49
x2=49
x=±7
զ) 3+x2=0
x2=-3
Ø
է) 8-2x2=0
-2x2=-8
2x2=8
x2=4
x=±2
ը) 3-12x2=0
-12x2=-3
12x2=3
x2=3/12=1/4
x=±1/2
թ) 7=28x2
1=4x2
x2=1/4
x=±1/2
ժ) ¼+x2=0
x2=-1/4
Ø
ի) x2-4/9=0
x2=4/9
x=±2/3
ա) x2-3=0
x2=3
x=±√3
բ) x2-5=0
x2=5
x=±√5
գ) 1/3x2-1=0
1/3x2=1
x2=3
x=±√3
դ) 1/5x2-10=0
1/5x2=10
x2=50
x=±√50
ե) 4x2-3=0
4x2=3
x2=3/4
x=±√3/4
զ) 5x2+3=0
5x2=-3
x2=-3/5
Ø
է) x2=2304
x=±48
ը) x2-31,26=0
x2=31,26
x=±√31,26
թ) 0,001x2=40
x2=40000
x=±200
ա) 4x2+6x=7x2-12x
4x2+6x-7x2+12x=0
-3x2+18x=0
x(18-3x)=0
x=0
18-3x=0
բ) 1,2x-0,5x2=4x2-0,8x
1,2x-0,5x2-4x2+0,8x=0
2x-4,5x2=0
x(2-4,5x)=0
x=0
2-4,5x=0
գ) 0,76x2+1,4x=0
x(0,76x+1,4)=0
x=0
0,76x+1,4=0
դ) 0,6x2+√3*x=0
x(0,6x+√3)=0
x=0
0,6x+√3=0
ե) 0,07x2-50=2,1x-50
0,07x2-50-2,1x+50=0
0,07x2-2,1x=0
x(0,07x-2,1)=0
x=0
0,07x-2,1=0
զ) 9x2-10x=7x2-15x
9x2-10x-7x2+15x=0
2x2+5x=0
x(2x+5)=0
x=0
2x+5=0
է) -0,5x2+√5*x=0
x(-0,5x+√5)=0
x=0
-0,5x+√5=0
ը) 2/3x2=5x
2/3x2-5x=0
x(2/3x-5)=0
x=0
2/3x-5=0
ա) (x-1)2+(x+1)2=2
x2-2x+1+x2+2x+1=2
2x2+2-2=0
2x2=0
x=0
բ) (x-7)(x+3)+(x-1)(x+5)+26=0
x2+3x-7x-21+x2+5x-x-5+26=0
2x2=0
x=0
գ) (3x-8)2-(4x-6)2+(5x-2)(x+2)=24
9x2-48x+64-16x2+48x-36+5x2+10x-2x-4-24=0
-2x2-8x=0
x(8-2x)=0
x=0
2x=8
x=4
դ) (2x-5)(3x-4)-(3x+4)(x-2)-10x-28=0
6x2-8x-15x+20-3x2+6x-4x+8-10x-28=0
3x2-31x=0
x(3x-31)=0
x=0
3x-31=0
3x=31
x=10.1/3
ե) (x+2)(x-3)(x-1)=x(x+1)(x+6)+6
(x2-3x+2x-6)(x-1)=x3+6x2+x2+6x+6
x3-x2-x2+x-6x+6=x3+7x2+6x+6
x3-2x2+5x+6=x3+7x2+6x+6
x3-2x2+5x+6-x3-7x2-6x-6=0
-9x2-11x=0
-x(9x+11)=0
x=0
9x+11=0
9x=-11
X=-11/9=-1.2/9
Առ․ 619/ա-դ/, 600, 601, 605
ա) 3x2-3=0
3x2=3
x2=1
x=√1
բ) 2x2=0
x2=0
x=√0
գ) x(x-1)=0
x=0
x-1=0
x=1
դ) x(x+3)=0
x=0
x+3=0
x=-3
ե) (x-3)(x+2)=0
x=3
x=-2
զ) (x+5)(x-7)=0
x=-5
x=7
է) 3x(x-0,5)=0
3x=0
X=0
x-0,5=0
ը) 0,5x(2+x)=0
0,5x=0
x=0
2+x=0
x=-2
թ) 3(x-8)(x+5)=0
x-8=0
x=8
x+5=0
x=-5
ժ) 0,8(x+1)(x-4)=0
x+1=0
x=-1
x-4=0
x=4
ա) x2-4x=0
x(x-4)=0
x=0
x-4=0
x=4
բ) x2+6x=0
x(x+6)=0
x=0
x+6=0
x=-6
գ) 3x2+x=0
x(3x+1)=0
x=0
3x+1=0
3x=-1
x=-1/3
դ) x2-0,5x=0
x(x-0,5)=0
x=0
x-0,5=0
x=0,5
ե) 2x+3x2=0
x(2+3x)=0
x=0
2+3x=0
3x=-2
x=-2/3
զ) x-2x=0
-x=0
x=0
է) 7x2=5x
7x2-5x=0
x(7x-5)=0
x=0
7x-5=0
7x=5
X=5/7
ը) 3x=11x2
3x-11x2=0
x(3-11x)=0
x=0
3-11x=0
-11x=-3 – 11x=3
x=3/11
թ) 1/2x2-3x=0
x(1/2x-3)=0
x=0
1/2x-3=0
1/2x=3
2x=6
x=3
ա) ax2+bx=0
բ) (x-a)(x+a)=0
գ) ax2+bx+c=0
a=b=c
ա) (x+8)(x-9)=-52
x2-9x+8x-72+52=0
x2-x-20=0
D=1+80=81
x1=1-√81/2=-8/2=-4
x2=1+√81/2=10/2=5
-4; 5
բ) (x-1)(2x+3)=7
2x2+3x-2x-3-7=0
2x2+x-10=0
D=1+80=81
x1=-1-√81/4=-10/4=-5/2=-2,5
x2=-1+√81/4=8/4=2
2; 2,5
գ) (x+1)(x+2)=(2x-1)(2x-10)
x2+2x+x+2=4x2-20x-2x+10
x2+3x+2=4x2-22x+10
x2+3x+2-4x2+22x-10=0
-3x2+25x-8=0
D=625-96=529
x1=-25-√529/-6=48/6=9
x2=-25+√529/-6=-2/-6=1/3
8; 1/3
դ) (x-1)(x-2)=(3x+1)(x-2)
x2-2x-x+2=3x2-6x+x-2
x2-3x+2-3x2+5x+2=0
-2x2+2x+4=0
D=4+32=36
x1=-2-√36/-4=-8/-4=2
x2=-2+√36/-4=4/-4=-1
-1; 2
Ուղղանկյուն եռանկյան սուր անկյան սինուսը, կոսինուսը, տանգեսը՝ SinA=CB/AB
SinA=CB/AB
COSA=AC/AB
tgA=CB/AC
SinB= AC/AB
COSB=CB/AB
tgA=AC/CB
SinA/COSA=CB/AB/AC/AB=CB/AC=tgA
COS2A+Sin2A=1
AC2/AB2+CB2/AB2=AC2+CB2/AB2=AB2/AB2=1
Առ․ 289, 290, 389
289.
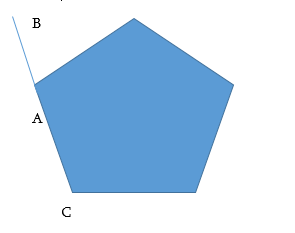
ա) <BAC=18°
Լուծում՝
180°-18°=162°
(n-2/n)*180°=162°
n-2*180°=162°n
180°n-360°=162°n
180°n-162°n=360°
18°n=360°
n=20
Պատ․՝ 20
բ) <BAC=40°
Լուծում՝
180°-40°=140°
(n-2/n)*180°=140°
n-2*180°=140°n
180°n-360°=140°n
180°n-140°n=360°
18°n=360°
n=9
Պատ․՝ 9
գ) <BAC=18°
Լուծում՝
180°-72°=108°
(n-2/n)*180°=108°
n-2*180°=108°n
180°n-360°=108°n
180°n-108°n=360°
72°n=360°
n=5
Պատ․՝ 5
դ) <BAC=60°
Լուծում՝
180°-60°=120°
(n-2/n)*180°=120°
n-2*180°=120°n
180°n-360°=120°n
180°n-120°n=360°
60°n=360°
n=6
Պատ․՝ 6
290.
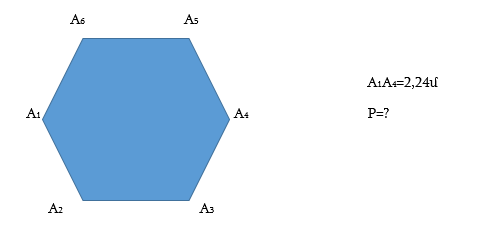
Լուծում՝
1) 2,24:2=1,12մ
2) 1,12*6=6,72մ
Պատ․՝ P=6,72մ
389. ա) SinA=7/25
COSA=AC/AB=24/25
tgA=CB/AC=24/7
SinB= AC/AB=24/25
COSB=CB/AB=7/25
tgA=AC/CB=24/7
1. Որ շրջանագիծն է կոչվում բազմանկյանը ներգծյալ:
Եթե բազմանկյան բոլոր կողմերին շոշափում է շրջանագիծը, ապա շրջանագիծը ներգծած է բազմանկյանը։
2. Որ բազմանկյունն է կոչվում շրջանագծին ներգծյալ:
Եթե բազմանկյան բոլոր անկյունները գտնվում են շրջանագծի վրա, ապա շրջանագիծն արտագծած է բազմանկյանը։
3. Ինչ հատկություն ունեն շրջանագծին արտագծյալ քառանկյան կողմերը:
Շրջանագծին արտագծած քառանկյան հանդիպակած կողմերի գումարն իրար հավասար են։
4. Ինչ հատկություն ունեն շրջանագծին ներգծյալ քառանկյան անկյունները:
Քառանկյան անկյունագծերի արտադրյալը հավասար հանդիպակած կողմերի արտադրյալների գումարին։
5. Որ բազմանկյունն է կոչվում կանոնավոր: Բեր օրինակ:
Այն բազմանկյունը, որի անկյունները իրար հավասար են և կողմերն իրար հավասար են, ապա այդ բազմանկյունը կոչվում է կանոնավոր։
Հնգանկյուն, քառակուսի, հավասարակողմ եռանկյուն․․․
6. Գրիր ուռուցիկ բազմանկյան անկյունների գումարի բանաձևը / n-անկյուն/ :
(n-2)*180°
7. Գրիր կանոնավոր բազմանկյան յուրաքանչյուր անկյան հաշվման բանաձև:
(n-2/n)*180°
8. Գտիր n-անկյան անկյունները, եթե n=10, բազմանկյունը կանոնավոր է:
(10-2/10)*180°=4/5*180°=144°
9. Քանի կողմ ունի կանոնավոր բազմանկյունը, եթե նրա յուրաքանչյուր անկյուն հավասար է 150 աստիճան:
(n-2/n)*180°=150°
n-2*180°=150°n
180°n-360°=150°n
180°n-150°n=360°
30°n=360°
n=12
10. Գտիր կանոնավոր քառանկյանը արտագծած շրջանագծի շառավիղը, եթե նրա կողմը հավասար է 5 սմ:
Լուծում՝
1) a²+b²=c²
2) √25+√25=√50=5√2
3) 5√2:2=5√2/2
Պատ․՝ 5√2/2
Լրացուցիչ:
1. Կանոնավոր վեցանկյան կենտրոնը միացված է գագաթներին: Ապացուցեք, որ առաջանում են վեց հավասարակողմ եռանկյուններ:
Կանոնավոր վեցանկյան թե՛ անկյունները, թե՛ կողմերն իրար հավասար են, հետևաբար կենտրոնից տարված հատվածները դեպի անկյուններ նույնպես հավասար են =>, որ վեցանկյան կենտրոնը միացնելով գագաթներին, առաջանում են վեց հավասարակողմ եռանկյուններ:
2. Գտեք շրջանագծին արտագծած և ներգծած քառակուսիների կողմերի երկարությունների հարաբերությունը:
Պատ.՝ 2:3
Թեմա՝ Կանոնավոր բազմանկյուններ
Ինքնուրույն աշխատանք
1. Որ շրջանագիծն է կոչվում բազմանկյանը ներգծյալ:
Բազմանկյանը ներգծած շրջանագիծ կոչվում է այն շրջանագիծը, որը շոշափում է բազմանկյան բոլոր կողմերի միջնակետերը:

2. Որ շրջանագիծն է կոչվում բազմանկյանը արտագծյալ:
Շրջագիծը արտագծած է բազմանկյանը, երբ բազմանկյան գագաթները անցնում են շրջանագծով:

3. Ինչ հատկություն ունեն շրջանագծին արտագծյալ քառանկյան կողմերը:
Շրջանագծին արտագծած քառանկյան կողմերի գումարները իրար հավասար են:
4. Ինչ հատկություն ունեն շրջանագծին ներգծյալ քառանկյան անկյունները:
Շրջանագծին ներգծյալ քառանկյան հանդիպակաց անկյունները իրար հետ կազմում են 180°:
5. Որ բազմանկյունն է կոչվում կանոնավոր: Բեր օրինակ:
Կանոնավոր է կոչվում այն բազմանկյունը, որի կողմերն ու անկյունները իրար հավասար են: Օրինակ՝ քառակուսի, վեցնակյուն և այլն:
6. Գրիր ուռուցիկ բազմանկյան անկյունների գումարի բանաձևը / n-անկյուն/ :
(n-2)*180
7. Գրիր կանոնավոր բազմանկյան յուրաքանչյուր անկյան հաշվման բանաձև:
(n-2)/n*180
8. Գտիր n-անկյան անկյունները, եթե n= 10, բազմանկյունը կանոնավոր է:
(n-2)/n*180=(10-2)/10*180=8/10*180=1440/10=144°
9. Քանի կողմ ունի կանոնավոր բազմանկյունը, եթե նրա յուրաքանչյուր անկյուն հավասար է 150 աստիճան:
(n-2)/n*180=150°
n-2/n*180/1=150°
180n-360=150n
180n-150n=360°
30n=360°
n=12
10. Գտիր կանոնավոր քառանկյանը արտագծած շրջանագծի շառավիղը, եթե նրա կողմը հավասար է 5 սմ:
Լուծում՝
AB2+BC2=AC2
25+25=AC2
AC=√50=5√2
5√2:2=5√2/2
Պատ․՝ 5√2/2
Լրացուցիչ:
1. Կանոնավոր վեցանկյան կենտրոնը միացված է գագաթներին: Ապացուցեք, որ առաջանում են վեց հավասարակողմ եռանկյուններ:
Պատ.՝ առաջանում են հավասարակողմ եռանկյուններ, քանի որ վեցանկյունը կանոնավոր է
2. Գտեք շրջանագծին արտագծած և ներգծած քառակուսիների կողմերի երկարությունների հարաբերությունը:
Պատ.՝ 2:3
Խնդիրներ ֆլեշմոբից՝
1*2*3*4 գրառման մեջ աստղանիշերը փոխարինեք գործողության նշաններով և փակագծեր օգտագործելով ստացեք բոլոր հնարավոր արժեքներից փոքրագույնը և նշեք այդ արժեքը:
1-2*3*4=(-23)
Պատ.՝ -23
2.Քանի՞ հատ քառանիշ թիվ կա, որոնց առաջին և երրորդ թվանշանների գումարը մեծ է 15-ից, իսկ երկրորդ և չորրորդ թվանշանների գումարը փոքր է 4-ից:
Պատ.՝ 60
3.Գտեք եռանիշ թվի և նրա թվանշանների գումարի հարաբերության հնարավոր ամենամեծ արժեքը:
100:1=100
Պատ.՝ 100
Առաջադրանքներ՝ 526, 535, 550
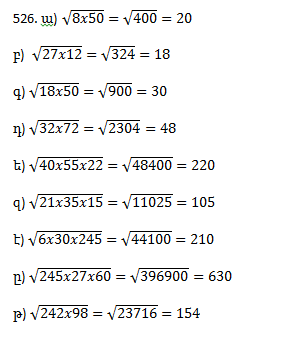
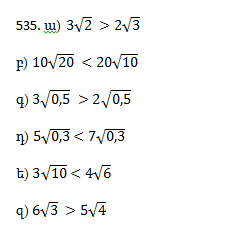

160.
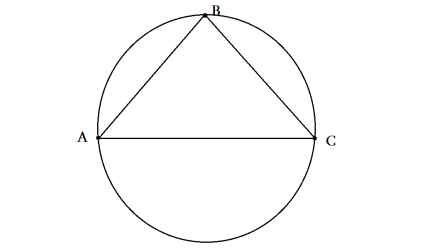
ա) Աղեղ AC = 48°
<B=?
<B=AC/2=24°
բ) Աղեղ AC = 57°
<B=?
<B=AC/2=28,5°
գ) Աղեղ AC = 90°
<B=?
<B=AC/2=45°
դ) Աղեղ AC = 124°
<B=?
<B=AC/2=62°
ե) Աղեղ AC = 180°
<B=?
<B=AC/2=90°
You can do it, too! Sign up for free now at https://www.jimdo.com